Category Archives: Other Continuous Line Artists

Change a four sided continuous structure into a single surface Mobius torus, or Mobioid.

Leave a reply

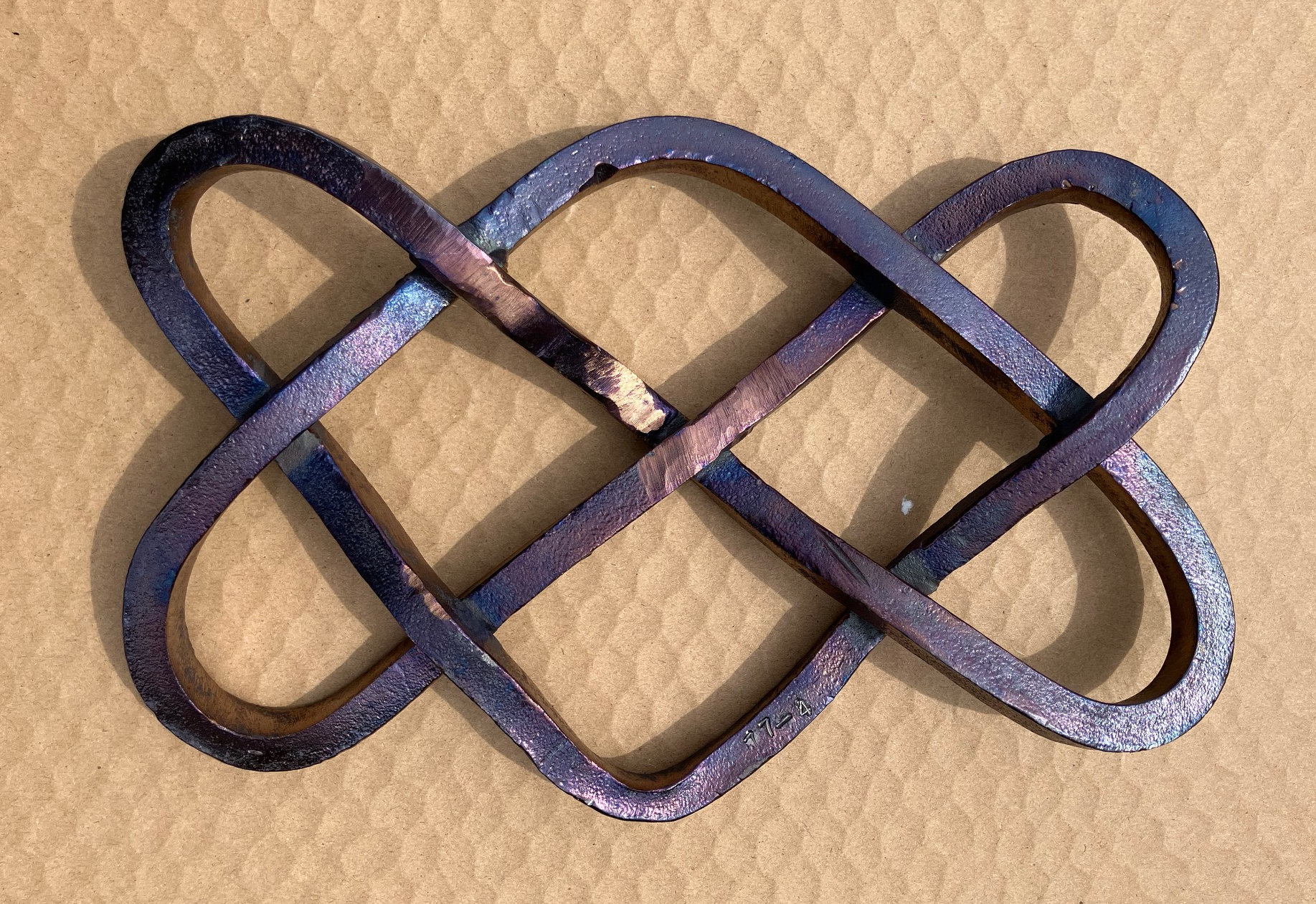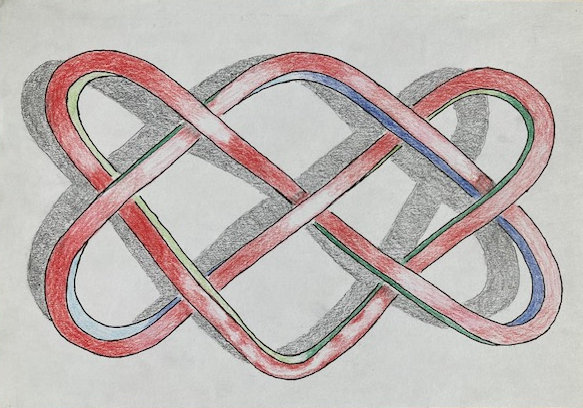
Drawing of Doug Eglen continuous metal sculpture with sides in four colours. Mick Burton, continuous line artist.

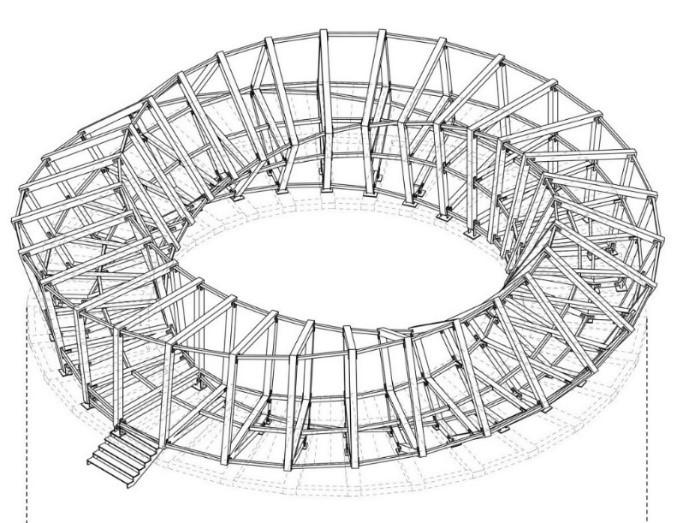
In my last post, on 3 June 2025, I said that I would like to draw Doug Eglen’s 3/8″ square forged metal sculpture. 

Continuous Lines in forged metal, by Doug Eglen.

Here it is, but I have used separate colours for each of the four sides.  You can only see Red, Green and Blue because the metal remains flat overall and you cannot see the Black I allocated for the underside.

I have tried to reflect the 3D quality of the sculpture, with its Celtic over and under style, highlights and shadow.

When I first saw the structure, I wanted to understand what would happen if I applied twists to the sculpture.  I thought that there should be one or more types of twist which would turn the culture from being four sided with four surfaces into four sided with one surface.  I knew that the Mobius Strip has two sides before the half twist and one continuous surface afterwards and thought that the single surface should also be possible for Doug’s structure.

Another thing that I wanted do was to try and clarify my idea that his structure reflected the shapes of two Boomerangs.  I wondered what twists I would need to do this.

The poker which I made at the age of 12 at school appeared to have a half twist but it is difficult to visualise how this changed the position of the sides.

Brass handle with half twist on my poker, made at school when I was 12. Mick Burton, continuous line artist.

I had to use a pencil to draw along one surface to confirm that it changed the top side into the bottom side.  This meant that I could use two half twists near the centre of a new drawing of the sculpture to produce two boomerangs which had individual colours.

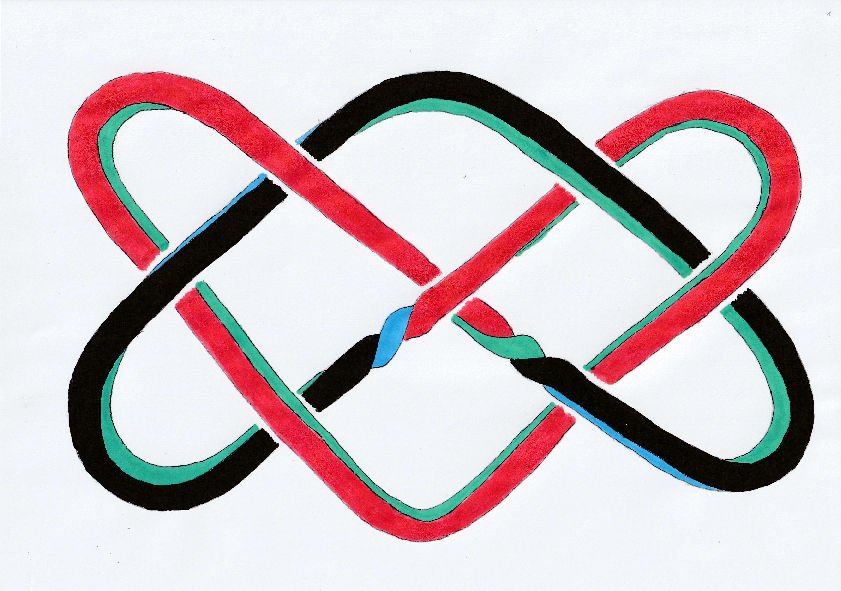
Using two twists to produce Black and Red Boomerangs on drawing of Doug Eglen’s metal sculpture. Mick Burton, continuous line artist.

Black has now appeared at the top for half the time, so we have four colours on view.  Another outcome is that the two sides, which are Green and Blue, swapped from one side to the other at the twists which has resulted in blue almost disappearing.  This is due to the close photographic angle by Doug showing most of the insides of each boomerang shape and I coloured them almost equally Green and Blue in my first drawing.  Green stayed the same within the Red boomerang here and Blue changed to Green in the new Black one.

I have mentioned the Mobius effect.  The Boomerang drawing has not produced a change in the number of surfaces but just altered their positions. Sides still equal surfaces.  This is because I have used two half twists.  If I had only used one half twist then the number of surfaces overall would become two surfaces, one colour for top and bottom and another for both sides.

It seemed to me that employing one quarter twist would produce a Mobius single surface throughout, as each time a surface comes round again it deflects a quarter and on the fourth approach it is back on top. Maybe a three quarter twist would also achieve this, but I found this more difficult to visualise.  First approach deflects to side 4, Second to side 3, Third to side 2 and fourth to side 1 again.

Anyway, I have drawn simply a single quarter twist as an addition to Doug’s sculpture.

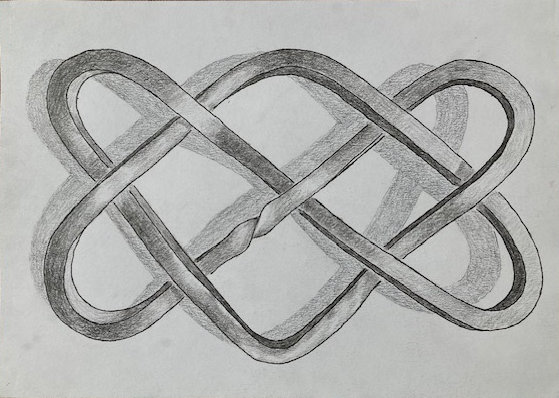
Drawing of Doug Eglen continuous metal sculpture, but with added quarter twist. Mick Burton, continuous line artist.

I have started with black and the result is All Black.  This drawing depicts a 4 sided metal continuous sculpture which has only one surface.  It is a complete Mobius result.  Visually, you can see that it is a quarter twist and our knowledge of the general sculpture helps us to realise that there is in fact one surface.

Yes, a Boomerang drawing and an “All Black” drawing suggest that I have Australian and New Zealand interests.  My mother, maiden name Brenda Mace, was born in a pub in Bedale, North Yorkshire.  Nearly 100 years earlier six brothers were born in the same pub and four of them went to gold fields in both Australia and then New Zealand in the early 1860’s.  They were cricketers as well and Christopher Mace played for Victoria against the first team to visit from England and two years later John and Harry joined with him, in Otago New Zealand, against the first English team to play there.

Back to the drawings.  I looked on the Internet for images of general structures which included a quarter twist and failed to find any.  There were examples of the pure circular twist, including 4 sided, but these are difficult to visualise as there is no obvious start point. 

Mobius Strip Structure of Rectangle Geometric Shape. Issuu website.

This pure circular twist is more understandable than most and the Issuu website shows how they built one which you can walk round in.  I am not sure if this includes walking upside down at one stage!

https://issuu.com/vsvu/docs/prof_is_1000/s/16586493

I feel that a twist anchored into an actual general structure, which has some straight and flat sections, is important.  It is easier to identify the type of twist and how the effect of the twist radiates through the whole structure in a more meaningful way.

Some other reference sites mention continuous surfaces, with more than the single edge and surface of a Mobius Strip, as Morbioids.  They compare their structure with the Torus (when it has parallel lines drawn around it which can be regarded as equivalent to edges which can produce the Mobius effect).

There are specific explanations of degree of twist, the number of sides, leading to the number of surfaces.  These confirm my assumptions about a quarter (90 degree) twist, or three quarter (270 degree) twist resulting in a single surface for the square structure.  A half (180 degree) twist has two surfaces.  Others explain 5 or 6 sides and there is a formula for n surfaces according to twist and sides.

A useful link that works is headed “Name for a 3 sided Mobius Strip?”  https://reddit.com/r/topology/comments/1bfdu7m/

SamwiseGanges    said that he was going to call them Mobius prisms.  When he referred to square Mobius prisms, he confirmed my assumptions about the effect of their twists.

AceThe Aro   said that Dr. Cye Waldman called them Mobioid’s in 2017 and you can click onto his moving images.  You can also click on Ace’s own slideshow which runs through all the different twist and number of sides possibilities.

I would like to refer to my drawing of Doug Eglen’s structure, with a quarter twist, as an “Anchored mobius torus”, or “Anchored Mobioid”.

Doug may consider loosening the join on his double boomerang ironwork and resetting it with a quarter (90 degree) twist.  That would produce a real single surface anchored Mobioid.  

 

 

Continuous Lines in forged metal, by Doug Eglen.

Leave a reply

Continuous Line knots in tempered metal forged by Doug Eglen. Photo by Doug sent to Mick Burton, April 2025.

Doug Eglen contacted me in March 2025 to say that he had recently started having an interest in knots and unknots and came across my painting of Haken’s Gordian knot, which you can see in my earlier posts of 9 May 2018 and 5 June 2015

Continuous Line Artist view of Haken’s Gordian Knot.

How do you construct Haken’s Gordian Knot?

He asked for my permission to paint his own version of the Gordian knot, based upon my painting.  He intended to exhibit his painting, along with the new metal knots which he was producing in his forge.  Doug has an exhibit case at Purdue University, Indiana, in the Math department library.  I agreed, and answered his questions about assumptions he had made about the construction of my painting. 

Doug later sent me a copy of his painting.  This is impressive, as are his metal knots, and you can see them on his website   

https://http://www.deglen.org/math-art

I particularly liked Doug’s photo of his 3/8″ square metal, in what I would call a sort of “double boomerang” shape without any twists.

Doug Eglen square 3/8″ metal without twists in a continuous line, copied to Mick Burton.

The alternate over and under style, like Celtic knotwork, produces great highlight graduations as well as suggestions of colour that Doug achieves with his firing treatments. I like the dark shade of the sides of the metal compared with the shadow of the piece.  I would like to draw this.

At school, when I was 12, I produced a metal poker with brass handle which has a half twist.  I have had no further experience of metal work.

Brass handle with half twist on my poker, made at school when I was 12. Mick Burton, continuous line artist.

I did do some wire bending to produce a single continuous line wire horse in 1967.  At first I placed it underneath a piece of clear glass covering the dining table, to hold it down.  Then I secured it to a wooden board through a centre page magazine photo of a horse grazing in a meadow.

Continuous line Horse in a length of garden wire done in 1967. Mick Burton.

Next, I went sculptural and used cardboard strips to take the Horse a stage further in 1970 when I lived in Nottingham.

Continuous line Horse using strips of cardboard 1970. Mick Burton.

I showed it to someone at work who’s Dad owned a company which produced steel castings. He said he would ask his Dad about the possibilities of doing a metal horse.  The answer was a “Yes”, but it would cost me £3,000 !  I now know someone who’s cousin does 3D printing, so maybe I can get a more reasonable quote now.

Of course, this is all “small beer” compared to Doug Eglen’s metal workings.

Continuous Line Drawing in Colour by Logan Clarke.

1 Reply

Logan's continuous line hen.

Continuous line Hen by Logan Clarke. Mick Burton post.

Logan contacted me a couple of months ago, saying that he was in Year 7 at a school in Derbyshire and that his Art Teacher had asked his class to complete a homework project based upon my art.

He liked the Rhino that I had featured recently (which was done by a member of Pateley Bridge Art club during a workshop) and my Hen with eggs, which I show below.  He asked for some advice on how I do my continuous line drawings.

Harriet’s Busy day. Single continuous line drawing with colour sequence. Background based on eggs. Mick Burton, 2012.

I sent Logan a short write up on my approach to Continuous Line Drawing and he later sent me his marvellous coloured drawing of his own hen invention, shown at the top of this post.  He has used a range of colours which go well together and the yellows are placed in a very balanced way.  He shows the vibrancy and character of the hen.

Logan’s Dad Paul also had a go at a continuous line Guinea Pig which I show below.

Logan’s Dad Paul Clarke’s continuous line guinea pig. Mick Burton post.

This is an excellent compact drawing with solid balanced colours.  I can imaging this animal bulldozing its way through the straw.

Logan had said that he was due to visit York on holiday and he was looking forward to doing a drawing of York Minster.  I said that I would like to see the result.  Here it is.

York Minster, drawing by Logan Clarke. Mick Burton post.

I mentioned to Logan that I have an ancestor, Thomas Mace a 17th century composer, who said in his book on music that he was at a service in the Minster during the Civil War when York was under siege by Cromwell’s soldiers.  He described how a small missile from a gun smashed through a high window and bounced off several pillars inside before hitting the floor.  Made me think of a pin ball machine.

 

Pateley Bridge Art Club Continuous Line Drawings

Leave a reply

Pateley Bridge Art Club member’s single continuous line Rhino with internal pattern.

I was at Pateley Bridge Art Club earlier this month with a Demonstration and Workshop for the members.  They have covered the evening in their News Blog with a report by Charles Mellor, which included 16 examples of members’ pictures.  You can find the report at >      https://www.pateleybridgeartclub.org      .

I include here an additional three pictures by members which illustrate how you can devise an internal pattern which represents aspects of the subject.  Members could base their initial attempt at a continuous line, or lines, on a subject of their choosing or one or more of several faint outlines provided by myself.

I demonstrated how the basic ongoing line can involve curves, loops, angles, etc. taking in parts of the outline itself and involving where possible a novel pattern for that subject.  At the same time there is a need to leave spaces for the line to return to the start.  I said that members were free to use rubbers to correct their drawings or have more than one continuous line in their picture to get used to the process.

One member drew a Giraffe which incorporated some of the distinctive inner pattern of that animal.

Giraffe by Pateley Bridge Art Club member, showing inner pattern.

My third example is a Zebra where the member has included the famous stripes.

Head of a Zebra, by Pateley Bridge Art Club member.

The Rhinoceros above has a good inner pattern reflecting the armour plating appearance of the animal.  It reminds me of the woodcut by Albrecht Durer, who was amongst the first artists to portray this animal.

Rhinoceros woodcut by Albrecht Durer in 1515.

And that’s not all.  The Pateley Bridge member’s Rhino at the top of this post has a clear single continuous line and includes two specific features I have used in the past which appear in pictures which I displayed on the evening but may, or may not, have have influenced the drawing of this Rhino –

a.  The Rhino’s left eye is depicted by a gap in the outline, similar to my Panther’s right eye below, where I show only the pupil of the right eye.   

Association of Animal Artists Annual Competition Winner !

b.  The Rhino’s armour pattern involves the outside running into the interior of the animal, similar to my Zebra below.

 

 

Continuous line Zebra without crossover lines.

Continuous Line Zebra

I have requested that the Pateley Bridge member, who did the Rhino, copies the line and then applies alternate shading to highlight the “inside outside” effect.  If not I may have to do it myself.

Picasso was certainly aware of this “inside outside” situation.  At my Demonstrations I pass around Picasso’s book “One-liners” which has 50 pictures.  Most have the line starting at one end and then stopping on completion elsewhere, but there are several which are single continuous lines.  The last two pen drawings in the book are as follows.

Picasso “Studies for Mercury”. Picasso’s One Liners. Artisan, 1997.

On the left, the head, arms, body and legs are all inside the single continuous line.  At first glance it is the same on the right, but in fact there is no “inside”.

Continuous Line Artist view of Haken’s Gordian Knot in “Unknot Hall of Fame”.

Leave a reply
  • Twisting, overlapping colouring of Haken’s Gordian Knot. Mick Burton single continuous line drawing painting 2015.

Peter Prevos, has included me in his “Unknot Hall of Fame”, within an article on his website about “The Art and Magic of the Trivial Knot”, which also explains many technical aspects of the trivial knot and how magicians have incorporated those ideas. There are designs, in the Hall of Fame, by Goeritz, Thistlewaite, Ochiai and Haken as well as art by Vanuatu and myself and reference to James Sienna. Have a look on – https://horizonofreason.com/science/unknot-gallery/

I had already done my painting when I saw a post on Mathoverflow website “Are there any very hard unknots?” by mathematician Timothy Gowers – https://mathoverflow.net/questions/53471/are-there-any=very-hard-unknots

I responded with posts on my website on in June 2015 and a later update in May 2018.

Noboru Ito, mathematician now at the of University of Tokyo, contacted me in February 2016 about his near completed book “Knot Projections” and my article is referenced in the Preface. “It was very helpful”.

Tomasz Mrowka, mathematician at the Massachusetts Institute of Technology, asked in November 2017 for a copy of my painting, as “it’s really quite striking and would love to hang it in my office”.

David Eppstein, computer scientist and mathematician at university of California, Irvine, featured my painting on his website in November 2018 “Mick Burton, an artist known for drawings that use a single continuous line to create the impression of complex and naturalistic shapes, looks at knot theory, self-overlapping curves, and the visualization of Seifert surfaces.” I had to look in Noboru Ito’s book to check out Seifert surfaces !

In essence my painting of Haken’s Gordian Knot is another example of me finding a well known structure which I can apply my continuous line knowledge and experience to. The way that nature can work in these structures often surprises me.

This is separate to my ongoing art work of producing single continuous lines and colouring based upon interesting subjects – which can be animals, landscapes, portraits, still life and abstracts.

Other examples of looking at structures have been –

Four colour theory maps, where my overdraw method could divide a map up into two streams of alternate colours, hence the four colours. I corresponded with mathematicians Robin Wilson and Fred Holroyd in the mid 1970’s. See my post in August 2015 on Skydiver patterns and my Four Colour Theory.

The artist Escher’s favourite tile at the Alhambra in Spain, which I realised had two continuous lines running through it. I saw that the artist could have made in into a single line with two small alterations. See my posts of April 2015.

Knights moves on a chess board starting and finishing at the same square and landing once on all the other squares. See my 1974 picture in the Gallery 1965-1974.

I am always on the look out for new structures which are suitable.

“Vortex” by David Kilpatrick. Single Continuous Line and Alternate Overdraw colouring.

Leave a reply

Vortex, David Kilpatrick. flat,1000x1000,075,f.u1

“Vortex” by David Kilpatrick, artist from Atherton, Australia.   Single Continuous Line using the Alternate Overdraw method to allocate colours.   March 2017.   Mick Burton blog.

I have been exchanging ideas with David Kilpatrick recently and he has agreed to let me put some of his pictures in my blog.  “Vortex” stands out to me, as I have been a fan of Vorticism for many years.  He has used Alternate Overdraw to allocate colours in sequence and it has worked well.

David’s design gives the impression of a sheet of plastic, coloured green on one side and red on the other, and each twist showing the other side.  With overlaps you get darker greens or darker reds.  Four internal areas let the background shine through.  The whole thing is very natural, including David’s own style of patchy colour radiating outwards.

Next is David’s “Knight’s Tour” which he is still working on.

David Kilpatrick knights tour. image011

“Knights Tour” by David Kilpatrick, artist from Atherton, Australia.   Single Continuous Line based upon moves of a knight and using Alternate Overdraw to allocate colour sequence.   April 2017.  Mick Burton blog.

I did a Single Continuous Line “Knight’s Moves on a Chessboard” in 1973 (see Gallery 1965-74) with the intention of colouring it, but never tackled it properly.  One of the problems was the number of fiddly small areas.  It led to my “Knight’s Tour Fragments” instead (see my previous post on 16.2.2017).

But now we have GIMP!  David said that he used this to move the lines about on his “Knight’s Tour”.  I googled GIMP and it means “GNU Image Manipulation Program”.  Some areas are still fairly small but he has produced a vibrant structure.

David says that these are trial colours (I presume from GIMP) and he intends to work out an improved scale of colours in his own style.

However, the colours shown already demonstrate the natural balance inherent in the Alternate Overdraw colour allocation.  The composition suggests to me an island with yellow “beaches” as well as reds within opposite “volcanic” zones.

There is a choice regarding background, which would naturally be the same colour as the light blue internal areas and result in a surrounding “sea”, or it could be left white as shown above.

I look forward to seeing the final version, which I am sure will be another splendid example of Vorticism.

Another picture that caught my eye was his “The Pram” which is based on a magic rectangle.

“The Pram” by artist David Kilpatrick, from Atherton, Australia.   Based on a Magic Rectangle. 2015.    Mick Burton blog.

This pram picture has lots of line ends in it and makes me want to attempt one myself using a Continuous Line animal.  Such a design would make you want to connect up so many loose ends.  My Spherical pictures already do this to an extent, as I take a line out of the picture at one side and bring it back in at the corresponding opposite side.

I think that David chose the positions of the displaced squares in a sort of random way.  Maybe I would want to be confident that I could move them around, in the way you could on the movable squares game of my childhood, and get back to the actual original picture.

You can see much more of the art of David Kilpatrick on

https://www.redbubble.com/people/fnqkid